Recently there was a need to have a body rotate around another moving body, sort of like a shield. To achieve this functionality, initially we thought of using a revolute joint, available in box2d in libgdx. For revolute joint we would need a base or pivot body around which another body can rotate at a fixed distance at fixed speed. We have already written a tutotial on this topic long back.
The above solution works fine when the base or pivot is a static body. As you can see in the heading, plan is to have the base body as either kinematic or dynamic. So that we base body can move if we give apply a force/impulse in case of dynamic body or set a velocity in case of kinematic body.
Physics of Uniform Circular Motion
We thought lets get into some physics to get this working. Lets first understand what we require. In our case we need uniform circular motion around a moving body. See below image for reference.
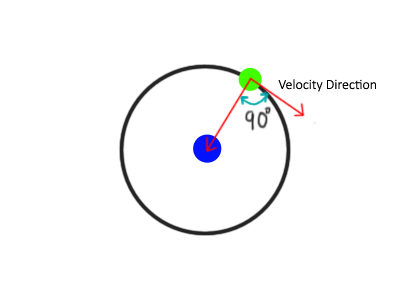
In our case velocity magnitude of the rotating body is initially defined and fixed. Second thing we require is to get the direction of velocity. As you can see the direction is parallel to the tangent of the circle i.e. perpendicular to direction. Lets calculate these vectors.
[sourcecode language="java"] body rotatingBody; body pivotBody; float velocity=100; Vector2 bodyDirection=new Vector2(rotatingBody.getPosition()).sub(pivotBody.getPosition()).nor(); float tangentAngle=-90; //to get velocity direction in clockwise motion with respect to pivot we need to rotate above direction vector by 90 degrees in anti clockwise direction Vector2 bodyVelocity=new Vector2( bodyDirection ); bodyVelocity.rotate(tangentAngle); //apply velocity to above velocity vector bodyVelocity.scl(velocity); [/sourcecode]
As our rotating body is a kinematic body, we can apply the above velocity in every frame to get circular motion. If we run the code using above velocity, we can see that the body starts to move in circular motion. But as time moves on it starts getting pushed outwards and the distance between pivot and rotating body keeps on increasing. This is happening because of the centrifugal force getting applied to the rotating body, which causes the body to move outwards.
Applying Centripetal Force
How to fix this? Well we delved into physics to understand that we need to apply a balancing centripetal force to keep the body at fixed distance. Similar to the tension a rope would have when tied to the rotating body as it is been thrown around. After some research we found a simpler way to do this. We are not going to guarantee it is the best solution but it should work.
Lets see below image and try to understand what we would need to get the rotating body at fixed distance from pivot. At every frame we calculate the new velocity of rotating body. The centripetal velocity will be change in distance from rotating body to center divided by time step i.e. 1/60 in our case. So we will calculate first the change in distance as below
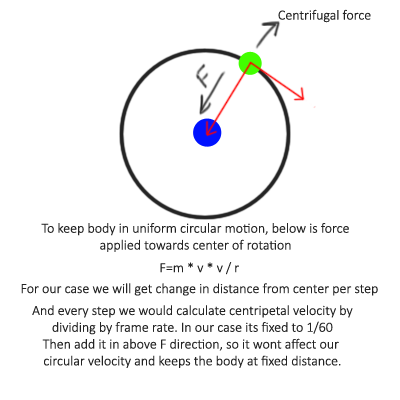
[sourcecode language="java"] float distance= rotatingBody.getPosition().dst(pivotBody.getPosition()); //Convert radius to box dimensions and get the difference float delta=distance-ConvertToBoxCoordinate(radius); [/sourcecode]
After we get the change in distance, we calculate centripetal velocity as follows.
[sourcecode language="java"] //Here we multiply by -1 to get centripetal direction //Then we divide by BOX_STEP which is equal to frame delta time Vector2 centripetlVelocity=new Vector2( bodyDirection ).scl(-1f*delta/BOX_STEP); [/sourcecode]
Calculate Final Velocity
Now we add both the above velocities to the rotating body as below
[sourcecode language="java"] Vector2 rotatingVelocity=new Vector2(); //Add fixed velocity tangent to the circular motion rotatingVelocity.set( bodyVelocity ); //Add centripetal velocity rotatingVelocity.add(centripetalVelocity); //Add pivot body's velocity to move rotating body along with the center rotatingVelocity.add(pivtoBody.getLinearVelocity()); [/sourcecode]
We can apply the above velocity to the rotating body to get uniform circular motion.
Here is link to Github Repository with full source code for the above example. Try it out and let us know if it helps you.